Le signe = , c'est comme une balance !

Le signe =, c'est comme une balance en équilibre. Il faut imaginer que de chaque côté du signe =, il y a un plateau de la balance. Il doit toujours y avoir des choses de même poids, c'est-à-dire des choses équivalentes, de chaque côté, pour que la balance reste en équillibre. 

Exemple :

---

Maintenant, on va modifier ce qu'il y a sur les plateaux de la balance, mais comme on veut qu'elle reste en équilibre, il faut qu'on fasse exactement la même chose des deux côtés ! On va donc diviser par 2 de chaque côté :

---

Si on n'avait pas fait la même chose de chaque côté, on aurait perdu l'égalité ou encore l'équilibre, comme sur l'image suivante :

---

On peut aussi faire autre chose que diviser(division) ou multiplier(multiplication) par la même chose de chaque côté : on peut en effet ajouter (addition) ou retirer (soustraction) la même chose de chaque côté. Dans l'image suivante, j'ai rajouté (addition) une carotte de chaque côté !

---

Comme avant, si on avait pas ajouté ou retiré exactement la même chose des 2 côtés, on aurait perdu l'équilibre ou l'égalité, comme sur l'image suivante :

---

Je pense que maintenant tu as compris le principe de la balance : si on veut garder l'égalité (c'est toujours ce qu'on veut faire en maths), on doit faire exactement la même opération de chaque côté du signe =.
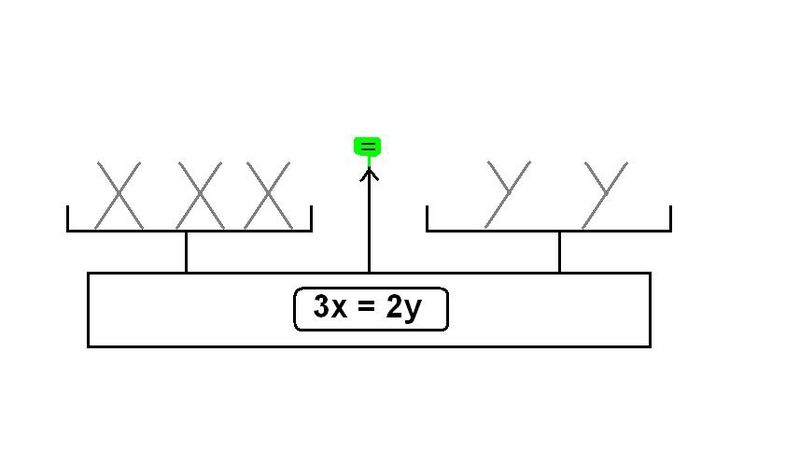
Tu vas voir que c'est vrai même pour des choses plus abstraites, comme des nombres ou même des lettres ! Regarde :

On voit que 3x sur un plateau "pèsent autant" que 2y sur l'autre plateau. C'est pourquoi on peut écrire 3x = 2y. 
Il ne faut pas se laisser impressionner par les lettres. 3x, c'est un peu comme 3 oeufs ou 3 carottes ! Pareil pour les y.

---

Maintenant tu vas voir qu'on peut toujours garder l'égalité si on fait exactement la même opération de chaque côté de la balance, ou plutôt de chaque côté du signe = 
Par exemple ici, on multiplie tout par 2 !

---

On aurait pu aussi très bien diviser de chaque côté par 2, même si ça ne tombe pas juste pour les x, et voilà ce qu'on aurait eu :

---

Et maintenant, on peut par exemple encore rajouter la même chose de chaque côté en gardant l'égalité. Allez, soyons fous, on rajoute une carotte de chaque côté !

on obtient donc 1,5x + carotte = y + carotte !

---

Par contre, si on avait pas fait la même chose des deux côtés, on aurait eu un déséquilibre, comme sur l'image suivante :

Ainsi, on trouve que 1,5x + 2 carottes, ce n'est pas égal à y + 1 carotte

---

Voilà, pour terminer, deux schémas en forme d'araignée, qui récapitulent tout ça. Ca marche pour les 4 opérations en maths, c'est-à-dire la multiplication, la division, l'addition, et la soustraction :

Tu vois qu'à partir de l'expression de base 7x = 4y, on peut faire plein de modifications, tant qu'on les fait de chaque côté.
On peut donc dire que 21x = 12y, ou encore que 0,7x = 0,4y, etc.

---

Ca marche bien sûr pour l'addition et la soustraction, comme on l'a déjà vu :

Ainsi, à partir de la même expression de base 7x = 4y, on peut faire des modifications tout en gardant l'égalité, il faut juste faire la même chose de chaque côté du signe = 
Par exemple, on peut dire que 7x - 35462 = 4y - 3562 !